들어가며
우리나라에도 제대로 된 온라인 뽑기 확률 계산기가 있으면 좋겠다는 생각에서 출발했었고, 주말을 투자해서 쓸만한 결과물을 얻었었다. 그리고 뽑기 확률 시뮬레이터 완성품에 대한 공개 및 계산 결과 해석방법에 대해서 이전 글에서 상세히 다루었다. 이전 글 링크는 다음과 같다.
https://projecteli.tistory.com/199
천장 찍으려면 얼마 필요? 뽑기 확률 시뮬레이터(Random box simulator)
뽑기확률 by ProjectEli (@projecteli) on CodePen. 작성계기 얼마전에 우연하게 확률형 아이템이 있는 게임들의 확률 표기 방식에 대해 문제를 지적하는 한 영상(김실장 유튜브)을 보고 영상에 나온대로
projecteli.tistory.com
이번 글에서는 해당 시뮬레이터를 구현한 과정에 대하여 적어 보겠다.
설계 동기 및 방향성
설계 동기
처음에 김실장 유튜브에서 소개된 일본 사람이 만든 것을 돌려보고 나서 든 생각은, 계산이 잘 되는건 알겠는데 왜 그런 결과가 나오는지 잘 모르겠다는 것이었다. 계산 원리라고 써있는게 이항분포 위키 링크밖에 없고 세부적으로 어떤 계산을 거쳐서 나오는지에 대한 언급은 전혀 없었다. 그 외에도 아무리 한자나 일본어에 익숙하다지만 역시 한글이 아니라서 읽을때 버벅거리니 번역기 돌려서 봐야 한눈에 들어오는게 너무 불편했다.
그리고 국내 자료들의 경우 검색을 약간 해보니 대부분이 위의 일본 계산기를 추천하거나, 아니면 엑셀같은걸로 구현을 해놔서 바로바로 쓰기가 어렵게 생긴게 많았다. 결과값 표시도 그다지 아름답지 못했다. 그나마 온라인용으로 쓸만한 게 와후리 사이트였는데 이것도 F12 눌러서 클라사이드 소스를 열어 보니 입력값을 서버로 보내서 계산하는 방식이었다. 계산 과정도 제대로 보여주지 않는데, 설령 결과가 맞는다 한들 어떻게 그 값을 믿을 수 있는걸까? 라는 의문이 들었다.
이쯤 되니 고등학교때도 배우는 이항분포 정도의 지식만으로도 계산이 가능해보이는데 왜 계산 과정을 좀 더 자세히 공개하지 않고 있는 거지? 너무 쉬워서 master equation만 있으면 되는건가? 라는 생각에 도달했고 별로 어렵지 않아보이니 내가 만들어도 좀 더 나은 계산기가 나올 수 있을 것 같았다. 그래서 개발을 시작하기로 했다.
설계 방향성
우리나라 사람이라면 누구나 쉽게 쓸 수 있도록, 그러면서도 결과값에 의심의 여지가 없도록 하기 위해 다음의 설계 목표들을 잡았다.
- 우리나라 사람이 보기 쉽게 우리나라 언어로 결과를 표시
- 접근성이 좋도록 웹브라우저에서 확인할 수 있게 구현
- 미려하고 간결한 디자인 사용으로 한눈에 알아볼 수 있도록 표시
- PC와 모바일에서 동일한 사용 경험을 얻을 수 있도록 모바일 친화적인 인터페이스 구현
- 특정 서버로 입력값이 전송되지 않도록 클라이언트 사이드에서 모든 계산을 수행
- 최종 예상 뽑기횟수 결과뿐만 아니라 개별 횟수에 대한 확률 계산 중간결과 등도 함께 제시
- 계산 원리 및 코드 공개를 통해 결과값의 신뢰도 향상 및 계산법 검증 도모
- 계산 결과 해석에 대한 가이드라인 제시
구체적 구현방안 마련
앞에서 정한 방향성을 구체적으로 어떻게 해야 구현할 수 있을 것인지에 대해 생각해 보았다.
- 언어를 한국어로:
내가 한국인이니 문제 없음. - 웹브라우저에서 구현:
html로 표시를 하고 연산 수행은 javascript 언어로 하면 js 하나로 모든게 정리될 수 있을 것으로 생각함. - 미려한 디자인:
이전부터 봐왔을 때 웹의 경우 부트스트랩(bootstrap)이 일관되고 호환성 문제가 적은 아름다운 UI를 제공하는 것으로 판단하였고, js native기 때문에 연동에 문제 없을 것으로 생각함. - 모바일 친화 인터페이스:
티스토리의 반응형 스킨이 화면 크기에 따라 UI를 자동 조정해 주므로 현재 블로그에 포스트로 작성하는 것이 여러 모로 유리하다고 판단함. - 클라이언트 사이드에서 계산 수행:
js를 이용해서 클라쪽에서 도는 코드를 잘 짜면 될 것으로 생각함. 다만 티스토리 블로그 및 웹브라우저에서 보안이슈로 페이지 내 자바스크립트를 허용하고 있지 않기 때문에 자체 페이지에 js를 넣는 것은 호환성 이슈가 생길 것으로 예상했고, 티스토리에서도 돌아가는 임베드 형식의 js 실행 플랫폼이 필요했음. 약간의 검색을 통해 CodePen이 그나마 지저분하지 않은 틀을 제공하고 유지보수가 잘 되며 향후 티스토리가 역변해도 격리된 공간에서 잘 돌아갈 것으로 예상함. - 확률 계산 중간결과 등도 함께 제시:
이것은 내가 구현하면서 결과표시에 추가하면 될 것으로 생각함. 디자인은 와후리 사이트처럼 진행바 형태로 표시하면 알아보기 쉬울 것으로 예상하였고, 와후리 사이트에서 오해가 생길만한 표현들이 있었는데 혼동을 방지하기 위해 단어 선택에 신중을 기해야 할 것으로 생각함. - 계산 원리 및 코드 공개:
원래는 GitHub 등에 코드를 업로드하고 링크하려고 생각중이었으나 CodePen을 써서 embed를 하면 자체 페이지에 코드까지 같이 나오게 되어있어서 더 좋을 것으로 판단하였다. 다만 사용자에게 코드가 바로 노출되면 지저분하니 탭을 눌러야 나오도록 정함 - 결과 해석에 대한 가이드라인 제시:
간결성을 추구하다보면 너무 간결한 나머지 이해가 안가는 경우가 나올 수 있는데 이를 보완하기 위해 결과 밑에 해석 방법을 쓰는 것으로 정함
구현 원리 및 계산 방법
여기에서는 최종 구현된 계산 방법에 대해 적어보겠다.
n번 시도시 k번 당첨될 확률 계산
독립시행이고 1번 시도할 때 당첨 확률이 p인 경우 기본 원리에 따르면 n번 시도했을 때 k번 나올 확률 P는 아래와 같이 이항분포 확률밀도함수 식으로 계산된다. 복잡한 용어는 이해에 방해만 되니 집어치우고 각 항의 의미에 대해 간단히 짚고 넘어가겠다.
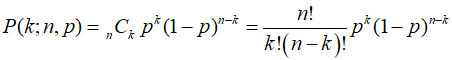
nCk = 당첨과 꽝의 2가지만 있는 경우에 n번을 뽑았을 때 나올 수 있는 모든 가능성 중 k번 당첨되는 경우가 몇 개인지
p^k (1-p)^(n-k) = 그렇게 k번 당첨되는 가능성 한 개가 나올 확률이 얼마인지
당첨과 꽝밖에 없으므로 꽝일 확률은 1-p이고, k번 당첨됐으면 꽝은 n-k번 나오므로 확률 식이 저렇게 되는 것은 어렵지 않게 이해할 수 있다. 이렇게 구한 k번 당첨되는 모든 경우의 수와, k번 당첨되는 가능성 한 개가 나올 확률을 곱했기 때문에 결과물은 k번 당첨되는 모든 조합이 나올 확률이 계산되는 것이다.
예를 들어 당첨확률 5%짜리 뽑기를 100번 돌렸을 때 정확히 3번 당첨될 확률은 다음과 같이 계산된다.
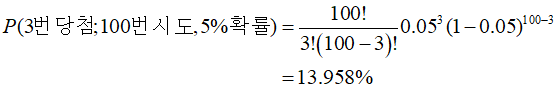
수학적으로는 깔끔하게 떨어지는 식이다. 그런데 이걸 컴퓨터로 구현할 때 문제가 발생한다. 바로 팩토리얼이 들어있기 때문.. 주목해서 봐야하는 게, 분자의 100 팩토리얼이다. 100번 시도만 해도 100 팩토리얼인데 이게 숫자가 어마어마하다. 대략적인 값은 9.33*10^157인데, 대충 158자리 숫자이다. 분모에도 97 팩토리얼이 있는데 이것도 만만찮게 크다.
컴퓨터에서는 숫자 하나에 배정하는 용량의 한계가 있기 때문에 표현할 수 있는 최대 숫자에 한계가 있다. 자바스크립트의 경우 다행히도 모든 숫자를 64비트인 배정밀도 더블로 표현하기 때문에 그나마 낫지만 그럼에도 약 1.798*10^308을 넘어가게 되면 더이상 정확하게 표현할 수 없게 된다. 수백 번만 뽑아도 팩토리얼 계산상으로 이 큰 숫자는 가볍게 넘겨버린다. 보통 뽑기할때 몇천 번은 자주 나오는 숫자인데 이 현상으로 인하여 문제가 커진다. 곱하고 나누는 연산 횟수가 많아질수록 정밀도는 점점 더 떨어지기 때문에 뽑는 횟수가 늘어날수록 정확한 확률 계산에 영향을 심각하게 미칠 수 있다.
그런데 분자 분모를 자세히 보면 이 식이 충분히 약분된다는 것을 알 수 있다. 이를 이용하면 연산 횟수를 획기적으로 줄일 수 있다.

이렇게 하면 계산할 때마다 발생하는 오차를 줄일 수 있고 분자 k번 분모 k번만 계산하면 되어 총 2k번의 계산으로 끝낼 수 있기 때문에 연산 속도도 빨라진다.
그리고 잘 보면 다음 조건을 만족하는 것을 알 수 있다.

이를 이용하면 분모중에 k가 클 경우 k!이랑 약분하고 k가 작을 경우 (n-k)!이랑 약분하면 계산 횟수가 최소한으로 줄어든다. 즉 k랑 n-k 중에 더 작은 수를 이용하면 좀 더 계산이 효율적이게 된다. 이를 수식으로 표현해보면 다음과 같다. 보통 k가 n에 비해 많이 작을 것이기 때문에 2k번으로 근사할 수 있다.
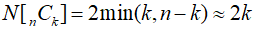
마지막으로 분자 분모를 따로 계산한 후 약분하면 각각이 매우 커질 수가 있기 때문에 오차가 발생할 수 있는데 계산할 때 그때그때 나눠주면 공학적으로도 오차가 줄어든다. 이를 모두 반영한 자바스크립트 함수는 다음과 같이 구현했다.
function binomial(n, k) {
if ((typeof n !== 'number') || (typeof k !== 'number'))
return false;
var coeff = 1;
k = Math.min(k,n-k);
for (let k2=1; k2<=k;k2++) {
coeff = coeff*(n-k2+1)/k2;
}
return coeff
}
최종 계산 결과는 정수로 나와야 맞는데, 계산 과정에서 정수만 나오지 않는 것을 알 수 있다. 그러나 자바스크립트는 모든 숫자를 double로 처리하므로 어차피 정수로 맞춰봐야 의미가 없다. 그리고 뒤쪽 확률하고 어차피 곱할건데 확률은 정수가 아닌 값이므로 미세한 오차는 충분히 무시 가능하다.
원래 식에서 뒤쪽의 확률 항에 대해서는 더 줄일수가 없기 때문에 그대로 계산한다. 이렇게 해서 총 연산횟수는 nCk에서 2k번, 확률계산에서 n번을 합해서 n+2k번 연산을 하게 된다. 수식으로 표현하면 다음과 같다.

물론 컴퓨터가 무지막지하게 빠르기 때문에 특정 k번이 당첨될 확률 구하는건 수백만번 뽑을때도 식은 죽 먹기로 매우 짧은 시간에 구할 수 있다. 보통 n이 k보다 훨씬 크기 때문에 대략 n번의 연산으로 끝낼 수 있다. 즉 이 계산의 속도는 대충 n이 2배 커지면 2배 오래걸린다고 생각할 수 있다.
n번 시도시 k번 '이상' 당첨될 확률 계산
앞에서는 정확하게 k번 당첨될 확률을 계산하는 방법에 대해서 다뤘는데, 어차피 뽑기할때는 정확하게 k번 당첨될 확률보다는 k번 이상 당첨될 확률을 구하는 것이 더 의미가 있을 것이다. 이것을 구하기 위해서는 0번부터 k-1번까지 당첨될 확률을 계산해서 1에서 빼주면 된다. k가 크면 뒤쪽부터 계산하는게 좋겠지만 보통 확률이 낮으므로 원하는 당첨횟수 k가 작을 것이기 때문에 앞쪽부터 계산해서 빼주는 것이 더 효율적일 가능성이 높다. 이를 수식으로 표현하면 다음과 같다. 주의할 점은 k번 이상이 필요하므로 k를 포함시키지 않는 k-1번의 확률까지 계산한 다음 1에서 빼주는 부분이다.
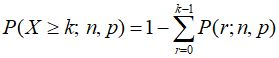
이를 구현한 자바스크립트 함수는 다음과 같다.
function calc_probs_partial(probvalue, trials, numwant) {
let problist = [];
let reciproc_probvalue = 1-probvalue;
// including zero win(+1), considering for loop k<max_k (+1)
let max_k = Math.min( Math.max(numwant,10), trials+2);
for (let k =0; k < max_k; k++) {
problist[k] = binomial(trials,k)*(probvalue**k)*(reciproc_probvalue**(trials-k));
}
return problist
}
function prob_notsuccess_partial(problist,numwant) {
var sum =0;
for (let k=0; k<numwant; k++) {
sum += problist[k];
}
return sum;
}
let prob_succeed = 1-prob_failed;위에서 probvalue = p, trials = n, numwant = k이다. 그리고 10회 미만의 당첨 횟수 목표를 적은 사람에게 좀 더 자세한 정보를 제공할 수 있도록 앞쪽 10개 정도는 필수로 계산하도록 했다.
calc_probs_partial에서 수행하는 연산횟수는 다음과 같다.

그리고 prob_notsuccess_partial 및 1에서 여분확률 빼주는 부분까지 하면 k번의 연산횟수가 추가되어 총 연산횟수는 다음과 같다.

k의 제곱에 비례하기 때문에 원하는 당첨횟수 k가 커질수록 계산량이 많이 늘어남을 알 수 있다. 그러나 보통 k보다 n이 매우 크기 때문에 대략 nk번과 유사하다고 보면 된다. n과 k를 곱한만큼의 연산량이므로 앞의 연산보다는 훨씬 오래 걸리는 것을 알 수 있다. 그래도 k가 작을 것이기 때문에 곱해봤자 몇백만 이하로 예상이 된다. 여기까지도 현대의 스마트폰 정도의 연산능력으로는 순식간에 계산해낼 수 있다. 문제는 다음이다.
k번 이상 당첨될 때까지 가능성이 y%인 예상 뽑기 횟수
보기에는 문장이 짧아서 간단해 보일 수 있는데 잘 보면 이게 간단한 문제가 아니라는 것을 알 수 있다. 먼저 k번 이상 당첨될 가능성이 r%인지 아닌지 판별하려면 n번 뽑는 경우를 상정하고 계산을 다 돌려봐야 알 수가 있다. 문제는 몇 번을 뽑아야 할지를 모른다는 것이다. 단순히 생각해도 당첨확률 0.01%짜리 뽑기를 99% 확정으로 먹으려면 엄청나게 많은 횟수가 필요할 것으로 예상할 수 있다. 뽑기 확률이 낮으면 낮을수록, 입력한 횟수만큼 당첨될 확률 목표가 높으면 높을수록 뽑아야 하는 횟수는 매우매우 커질 수 있다. 이러한 상황에서 1번 뽑기부터 언제 끝날지 모르는 y% 나올때까지 뽑기 횟수를 늘리다가는 연산 자원이 남아나지 않을 것이다.
실제로 와후리 사이트가 확률값에 매우 작은 숫자를 넣어버리면 계산 결과를 받아보기까지 매우 오랜 시간이 걸리는 것으로 보아 이 방식을 사용하는 것으로 추정할 수 있었다.. 그런데 2번 이상 반복적으로 계산하는 경우 바로 답을 주는 것을 보면 자체 서버에서 계산 결과를 캐싱하는 것으로 추측해볼 수 있었다. 그런데 이전 글에서도 언급했듯이 이렇게 되면 누군가가 무슨 확률을 돌리는지 서버 쪽에서 정보를 모을 수 있기 때문에 보안상 그다지 좋지 않을 수 있다.
반면 일본 사이트의 경우 확률에 작은 숫자를 넣더라도 거의 즉각적으로 계산결과가 나왔다. 어떻게 했는지에 대해서 설명을 찾아봐도 잘 찾아지지가 않았다. 나도 무지성으로 1번 뽑기부터 서서히 늘려가는 방식을 시도해 봤는데 확률이 0.1%만 되어도 계산시간이 몇 초 이상, 0.01%면 수십 초 이상 걸려버리는 현상을 겪었다. 이대로라면 국내 확률형 아이템 중 1퍼센트 미만에 대해서는 계산 눌러놓고 결과 기다려야 하는 시간때문에 매우 귀찮아지는 상황이 자주 나오게 될 것으로 예상했다.
도대체 일본 사이트는 어떻게 빨리 계산한 것일까? k번 이상 당첨되기 위한 확률 계산은 위에서 언급한 바와 같이 개별 확률을 다 더한 결과이다. 다시 가져와보면 아래와 같다.

전문용어로는 cumulative distribution function (CDF) 이라고 하는데, n이 바뀔때마다 summation을 다시 계산해야 한다면 너무 많은 연산량을 요구하기 때문에 오른쪽 항의 sum부분을 어떻게든 sum이 아닌 연산량이 더 적은 형태로 바꿔 주는 것이 필요하다. 그런데 이항분포같이 단순한 경우에도 이것을 더 간단한 식으로 정리하는게 말처럼 쉽지 않다. 이건 완전 수학이기 때문에 관련 지식이 없는 나로서는 유도해내지 못하였다. 그래도 이미 눈앞에 빠르고 정확하게 계산되는 일본 계산기가 있기 때문에 뭔가 방법이 있을 거라고 생각했다.
약간 찾아보니 beta function과 incomplete beta function이란걸 이용하면 직접 더하는 것 대신 적분식으로 정확하게 계산할 수 있는데 막상 적분을 프로그래밍으로 구현하려면 구분구적법같은걸 써야 해서 또 오차가 발생하게 된다. 이렇게는 안되겠다고 생각할 때쯤, 이에 관해 힌트를 얻을 수 있는 stackoverflow 글을 발견했다. python 코드를 보면 다음과 같다.
import numpy as np
def binomial_cdf(x,n,p):
cdf = 0
b = 0
for k in range(x+1):
if k > 0:
b += + np.log(n-k+1) - np.log(k)
log_pmf_k = b + k * np.log(p) + (n-k) * np.log(1-p)
cdf += np.exp(log_pmf_k)
return cdf
계산 내용을 보면 log로 계산하고 마지막에 exponential에 넣어버리는데 이항분포 정의 식을 통째로 로그를 취했다고 볼 수 있다. 즉 해당 글에서 exact라고 하는 것이 수학적으로는 정말 맞다는 얘기다. 이렇게 하면 확률 계산에서 n번가량의 거듭제곱이 들어갔던 부분이 로그에서 단순 곱셈으로 바뀌면서 n에 관한 연산량이 단 몇 번으로 줄어들게 된다. 왜 이걸 생각을 못했을까?
다만 이렇게 하면 생기는 실제 계산상에서의 한계점은 log로 한번 갔던 숫자를 곱하거나 더하는 과정에서 유효숫자가 깎여나가고, 그 결과를 또 exp에 넣기 때문에 정확도가 약간 낮아질 수 있다. 특히 이 결과를 누적해서 더하기 때문에 더하는 횟수가 많아질수록 오차가 커질 수 있다. 두 번째 한계는 n에 비례하는 연산량을 log를 사용하게 되면서 k에 비례하는 연산량에 곱셈으로 전가시켰다는 점이다.
연산량을 계산해 보면 k당 coefficient를 계산하는 데 덧셈 1번 log 2번+ 뺄셈 1번으로 3번, 확률을 계산하는 데 덧셈 2번 곱셈 2번 로그 2번 해서 6번, 그리고 마지막으로 exp 계산하는데 1번 추가다. 즉 10k의 연산량이 필요하다는 것이다. 앞에서 로그 안쓰고 할 때에 대략 nk번이었던 것을 생각하면 n이 10 보다 크기만 하면 연산횟수로는 대충 이득이다.

하여간 이 계산방법을 아래와 같이 자바스크립트 코드로 포팅하였다.
function binocdf_upper(x,n,p) {
let cdf=0;
let b=0;
for (let k=0; k<=x; k++) {
if (k>0) {
b = b+ Math.log(n-k+1) - Math.log(k);
}
cdf = cdf+ Math.exp(b+k*Math.log(p) + (n-k)*Math.log(1-p));
}
return 1-cdf;
}
문제는 여기서 끝이 아니라는 것이다.
n이 몇으로 해야 원하는 횟수를 뽑을 확률이 y% 이상이 나오게 하는지를 알 수가 없기 때문에 일일이 시도해야 하는 문제는 아직 남아있었다. 위 코드를 적용하면 분명히 빨라지기는 했지만 여전히도 작은 당첨확률, 즉 예상 n이 큰 경우에 대해서는 오래 걸리는건 마찬가지였다.
그래서 특단의 조치로 10배 단위로 구간을 쪼개는 방법을 선택했다. 일본 사이트처럼 뽑기 횟수 상한을 100만번으로 놓고(보통 이거보다 많이뽑을 사람이... 아마 없지않을까) 10배 단위로 하면 1부터 1e6까지 총 7개의 테스트 지점이 생긴다. 각 지점에서 k번 이상 뽑을 확률을 계산해서 y%랑 비교해보면 확실히 아닌 구간은 제외할 수 있을 것으로 생각했다. 여기에서 얻은 집중해야되는 구간에서 균등 정수 간격으로 최대 1001포인트를 찍은 다음 확률에 대한 linear interpolation을 하면 대략적으로 목표 당첨횟수 달성확률이 y% 근처가 나오는 예상 뽑기 횟수를 얻을 수가 있다.
n이 1000보다 작다면 당연히 정확할 것이고, 그것보다 큰 경우에도 100만 이하라면 n에 따라 단조증가하는 확률값 특성상 linear interpolation이 꽤 정확하게 예측해 주는 것으로 파악했다. 더 정확하게 하려면 interpolation해서 나온 결과 근처에서 다시 오차가 적어지는 방향으로 n을 바꿔가면서 찾으면 되는데, 보통 요구 n이 이정도로 크다면 현실적으로는 아주 정확한 수치는 필요 없을 것으로 생각하여 설령 오차가 약간 생기더라도 무시 가능할 것으로 보고 구현하지 않았다. 관련 자바스크립트 구현 부분은 아래와 같다.
---- (2022-05-26 내용변경) ----
이전에 만들었던 내용에서 10배 단위로 쪼개서 테스트하고 1001개로 linear interp하는 방법을 시도했었는데 숫자가 커질수록 오차가 발생할 수 있고 애초에 100만개보다 많이뽑아야 하는 경우에 올바르지 않은 결과를 줄 수 있었다. 최근 binary search라는 알고리즘을 접했고, 그것이 더 일반적으로 정확하고 효율적인 방법으로 판단이 되었기 때문에 코드를 수정했다. 또한 얼마 전 무슨 게임에서 0.00008%인가 하는 매우 작은 확률로 드랍되는 아이템으로 블로그 검색 유입됐던 것을 확인해서 수정하는 김에 표시되는 요구 뽑기 횟수의 상한도 100만에서 2^31-1로 크게 상향하였다. 그리고 변수명도 리팩토링 하였다. 관련 코드는 다음과 같다.
function buildRequiredTrialsTable(probabilityPerTrial,targetWinnings,costPerTrial,costUnit,targetProbPercentList) {
const targetProbPercentListLength = targetProbPercentList.length;
let targetProbList = []; // target Probs to be displayed
for (let k=0; k<targetProbPercentListLength; k++) {
targetProbList.push(targetProbPercentList[k]/100); // percent to actual number
}
let requiredTrials = [];
// binary search
const MAX_TRIALS = 2**31-1;
for (const targetProb of targetProbList) {
let trialsLowerBound = 1;
let trialsUpperBound = MAX_TRIALS;
do {
const testTrials = Math.floor((trialsLowerBound + trialsUpperBound) / 2);
if (testTrials === trialsUpperBound) { // select upper bound
requiredTrials.push(trialsUpperBound);
break;
}
const testProb = binocdf_upper(targetWinnings-1, testTrials, probabilityPerTrial);
if (targetProb - testProb >= 0) { // correction to upper side
trialsLowerBound = testTrials + 1;
}
else { // correction to lower side
trialsUpperBound = testTrials - 1;
}
} while (trialsLowerBound <= trialsUpperBound );
}
//build table
let tb = probTableTemplate("달성 가능성","요구 뽑기 수","예상 비용");
for (let k=0; k<requiredTrials.length; k++) {
var tr = tb.insertRow();
let targetProb = targetProbPercentList[k];
if (targetProb == 50) {
tr.className = "table-info";
}
else if (targetProb == 80) {
tr.className = "table-success";
}
else if (targetProb == 90) {
tr.className = "table-warning";
}
else if (targetProb == 95) {
tr.className = "table-primary";
}
else if (targetProb == 99) {
tr.className = "table-danger";
}
let requiredTrial = requiredTrials[k];
let expectedCost = requiredTrial*costPerTrial;
setRowContentRequiredTrials(tr, targetProb+"%",requiredTrial+"회",
expectedCost.toString()+costUnit);
}
return tb;
}
---- (2022-05-26 내용변경 끝) ----
여기까지 해서 계산을 하니 빠른 시간 안에 아주 잘 결과가 나오는 것을 확인할 수 있었다. 몇개 입력값에 대해 일본꺼랑 비교도 해봤는데 같은 값을 얻는 것으로 확인하여 계산도 맞게 하는걸로 검증되었다고 볼 수 있게 되었다. 휴.. 힘들었다.
UI 디자인
사용자 입력 창
사용자 앞에서 설명한 대로 bootstrap을 쓰면 쉽게 해결된다. 예제도 잘 되어있어서 부트스트랩 문서를 참고해서 CodePen의 JS에 import를 시켜 주었고 입력창에 input group mb-3와 btn-success 클래스를 이용해서 다음과 같이 구성했다.
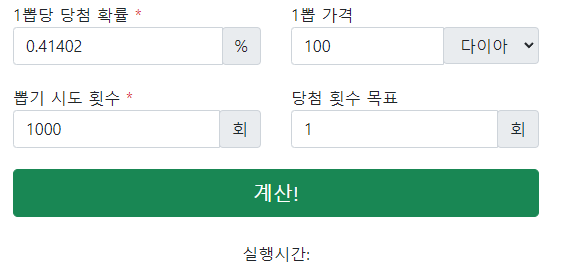
일본 사이트와 국내 사이트 둘 다 위와 같은 형태를 취하고 있어서 적당히 벤치마크를 해서 세부 조정을 마쳤다. 역시 부트스트랩이 대충 만들어도 깔끔하게 잘 만들어지는 것을 체감할 수 있었다. 단어 선택은 뽑는 것과 뽑히는 것 으로 하기보다는 뽑는 것과 당첨으로 명확하게 구분하였다.
계산 버튼
다른 사이트들에서는 버튼에 post명령을 쓰게 되어 있었지만 나는 외부 서버와 통신하는 것이 아니므로 그냥 jQuery로 클릭시 함수를 실행하는 listener를 달아 주었다. 문제는 계산 시간이 오래 걸리는 경우 대기 창이 나오도록 코드를 넣었는데, 이게 분명히 맞게 짰는데 막상 오래걸리는 계산에서 화면이 굳어버리고 계산 다 끝나야 나오는 것이었다. 그래서 이것저것 해보다가 결국 대기창 나오고 0.5초 후에 계산을 시작하게 만드니 드디어 나왔다. 웹은 역시 이해가 안되는 이상한 현상이 많은 것 같다. 관련 코드는 아래와 같다.
$("#btn-prop-calc").click(function(event){
$('input').prop('disabled',true);
$("#btn-prop-calc").prop('disabled',true);
$("#prop-calc-result").addClass('hidden');
$('#loader').removeClass('hidden');
setTimeout(MainWork,500);
}
);
계산 결과창
와후리 사이트에서 확률 결과를 정확히 k번 뽑는 경우와 k번 이상 뽑는 경우를 섞어서 보여주는 점이 마음에 들지 않았어서 나는 두 경우를 분리해서 다음과 같이 표시했다. 첫 번째 표에서 목표 달성률을 확인시켜주고, 두 번째 표에서 정확히 k번 뽑는 기대 확률과 해당횟수 이상 당첨률을 차례로 표시해 주어 혼동을 방지하였다.

그리고 다음과 같이 이 계산기를 만들려고 했던 핵심 데이터인 예상 뽑기 횟수를 각 %별로 표시하였다. 이 때 다른 사이트들에서 95%가 없어서 내 계산에는 95%도 넣었다. 예전에 메이플 할때 70% 주문서가 일요일에 확률 95%까지 올리는 버닝 타임?같은게 있었는데 그런 걸 보면 확정적=95% 정도로 해석할 수 있을 것 같아서 이 숫자도 중요하다고 생각한다. 마지막으로 계산하는데 걸리는 시간도 계산이 끝난 후에 맨 아래에 표시해주었다. 이로써 이틀간의 개발 작업이 완료되었다.

티스토리로 시뮬레이터 결과물 embed
처음 설계 당시 CodePen이 티스토리에서 잘 작동된다는 것은 알았고, 실제로 다 만들고 embed해 보니 확률 계산 및 결과 표시 동작에는 이상이 없었다. 그런데 내용이 세로로 많이 길쭉해져서 조막만한 곳에 세로 스크롤바가 생겼다. 빈공간에 스크롤바만 있으면 좋았겠지만 CodePen 로고가 마패처럼 떡하니 자리잡고 있어서 실제 컨텐츠가 보이는 공간은 더욱 비좁아졌다. 그래서 html 코드상으로 iframe의 height를 충분히 길게 주니 PC버전에서는 정상적으로 표시되었으나 모바일에서 열면 티스토리 반응형 스킨인 Odyssey의 자체 리사이징 기능때문에 자꾸 세로가 300으로 고정되었다. CodePen이 세로로 늘어날때 티스토리 스킨이랑 호환성이 안좋을줄은 전혀 예상하지 못했다...
이걸 고치기 위해 문서에 script 태그로 JS를 넣어서 해결해보려 했으나 이 글 초반부에 말한 보안 이슈로 제대로 실행되지 않았다. 방법을 좀 더 찾아보았으나 무슨 짓을 해도 티스토리 스킨의 css가 최우선 적용되는 바람에 모바일에서 세로로 찌부러져있는 현상이 해결되지 않았다.
결국 문제되는 부분을 찾아서 다음과 같이 Odyssey 스킨 css의 높이 제어 부분을 비활성화시키는 것으로 잠정 해결하였다.
/* area_view - 유튜브 사이즈 제어 */
@media screen and (max-width: 743px) {
.article-view iframe {
width: 100%;
/* height: 56vw; codepen 줄어드는거때문에 넣음 Eli*/
-ms-height: 56vmax;
}
}이렇게 했더니 모바일에서 내 블로그에 넣은 유튜브 embed들이 재생시 화면을 뚫어버리거나 검은색 레터박스가 크게 생기는 현상이 나타났는데, 어차피 앞으로도 유튜브 영상을 바로 재생할 수 있게 embed할 일이 거의 없을 것 같아서 이 상태로 쓰기로 했다.
구현 후기
위의 내용을 쭉 읽었다면 알겠지만, 역시나 상상과 실전의 난이도 차이는 컸다. 결국 다 구현하고 나니 이항분포 기본 식 외의 별다른 수학적 지식은 필요가 없었고, 나머지는 전산학에서 말하는 엔지니어링과 퍼포펀스 최적화 관련으로만 검색을 열심히 했던 것 같다. 그래도 이틀 정도에 구현을 했고 반나절 정도에 위와 같이 정리할 수 있어서 적당히 도전해볼만한 프로젝트였다고 생각한다. 코드상으로 변수명 등등 너무 두서없이 막 짜서 리팩토링을 하고싶긴 한데, 일단은 잘 돌아가기도 하고 퍼포먼스상에 문제도 없어서 계산상 중대한 문제가 발생하거나 나중에 여유로워질 때 고치기로 정했다. 사실 나도 본업이 있는 사람이라 원래 이런 글 쓸 시간도 아껴야 되는게 맞는데, 생각날 때 정리 안해두면 고민했던 흔적들과 해결방법이 언제 휘발되어 날아갈지 몰라서 일단 붙잡고 쓴 것 같다.
하여간 간만에 js 프론트엔드를 다시 공부해볼 수 있는 기회가 되어서 좋았고, 결과물도 나름 남들이 별로 안하고 있었지만 공익을 위해서 필요한 기능이라고 생각해서 보람 있는 행동이었던 것 같다. 구현 원리에 대해서 정리한 이번 글도 누군가에게는 도움이 되지 않을까?
혹시 구현 내용에 대해 의견이 있거나 궁금한 점이 있는 경우 댓글 등으로 제보해주면 고맙겠다. 그럼 여기까지.
'IT > 새로운 시도' 카테고리의 다른 글
| 그림 그리는 AI, 나도 그냥 쓸 수 있게 된 세상. Stable Diffusion으로 세상에 없던 그림 만들기 (3) | 2022.10.20 |
|---|---|
| 윈도우에서 한글 음성명령을 위한 VoiceMacro 세팅법 (0) | 2022.07.22 |
| 천장 찍으려면 얼마 필요? 뽑기 확률 시뮬레이터(Loot box simulator) (6) | 2022.01.17 |
| 논문용 멋진 그림 그리는 법에 관한 자료 (7) | 2021.12.16 |
| 화상회의, zoom 대신 써보는 MS teams (0) | 2021.11.25 |